川沙中学高中二年级期末数学试题
2020.01
1、 填空题
1. 椭圆![]() 的焦距等于__________
的焦距等于__________
2. 双曲线![]() 的渐近线方程是__________
的渐近线方程是__________
3. 若线性方程组的增广矩阵是![]() ,其解为
,其解为![]() ,则
,则![]() __________
__________
4. 已知复数![]() ,则
,则![]() 的虚部为__________
的虚部为__________
5. 圆![]() 的圆心到直线
的圆心到直线![]() 的距离等于__________
的距离等于__________
6. 若复数![]() (
(![]() ),若
),若![]() ,则
,则![]() __________
__________
7. 已知向量![]() ,
,![]() ,
,![]() ,若
,若![]() ∥
∥![]() ,则
,则![]() __________
__________
8. 参数方程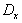 (
(![]() 为参数,且
为参数,且![]() )化为普通方程是__________
)化为普通方程是__________
9. 已知直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,
,![]()
__________
10. 若椭圆![]() 上一动点
上一动点![]() 到定点
到定点![]() (
(![]() )的距离
)的距离![]() 的最
的最
小值为1,则![]() __________
__________
 11. 设
11. 设![]() ,过定点
,过定点![]() 的动直线
的动直线![]() 和过定
和过定
点![]() 的动直线
的动直线![]() 交于点
交于点![]() ,则
,则
![]() 的最大值是__________
的最大值是__________
12. 在平面直角坐标系![]() 中,点
中,点![]() 是坐标原点,点
是坐标原点,点
![]() 、
、![]() ,点
,点![]() 在圆
在圆![]() 上运动,
上运动,
若![]() ,则
,则![]() 的最小值为__________
的最小值为__________
2、 选择题
13. 关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() ,其中行列式
,其中行列式![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
14. 已知复数![]() ,
,![]() (
(![]() 为虚数单位),在复平面内,
为虚数单位),在复平面内,![]() 对应的点在( )
对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
15. 设![]() 、
、![]() 均在双曲线
均在双曲线![]() 上运动,
上运动,![]() 、
、![]() 分别为双曲线的左、右焦点,则
分别为双曲线的左、右焦点,则
![]() 的最小值为( )
的最小值为( )
A. ![]() B. 4 C.
B. 4 C. ![]() D. 以上都不对
D. 以上都不对
16. 已知椭圆![]() 的焦点为
的焦点为![]() 、
、![]() ,过
,过![]() 的直线与
的直线与![]() 交于
交于![]() 、
、![]() 两点,若
两点,若
![]() ,
,![]() ,则
,则![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3、 解答卷
17. 设![]() 为关于
为关于![]() 的方程
的方程![]() (
(![]() )的虚根,
)的虚根,![]() 为虚数单位.
为虚数单位.
(1)当![]() 时,求
时,求![]() 、
、![]() 的值;
的值;
(2)若![]() ,在复平面上,设复数
,在复平面上,设复数![]() 所对应的点为
所对应的点为![]() ,复数
,复数![]() 所对应的点为
所对应的点为![]() ,
,
试求![]() 的取值范围.
的取值范围.
18. 过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于点
的直线交抛物线于点![]() 、
、![]() (其中点
(其中点![]() 在第一象限),
在第一象限),
交其准线![]() 于点
于点![]() ,同时点
,同时点![]() 是
是![]() 的中点.
的中点.
(1)求直线![]() 的倾斜角;
的倾斜角;
(2)求线段![]() 的长.
的长.
19. 直线![]() 与双曲线
与双曲线![]() 相交于不一样的两点
相交于不一样的两点![]() 、
、![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
20. 已知两点![]() 、
、![]() ,动点
,动点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 、
、![]() 的两个斜率存在,分别记为
的两个斜率存在,分别记为![]() 、
、![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹有两个交点
的轨迹有两个交点![]() 、
、![]() ,当
,当![]()
时,求直线![]() 的方程.
的方程.
21. 已知两点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,记
,记![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() (
(![]() )交曲线
)交曲线![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() 并延长交曲线
并延长交曲线![]() 于点
于点![]() .
.
(1)求曲线![]() 的方程,并说明曲线
的方程,并说明曲线![]() 是什么曲线;
是什么曲线;
(2)若![]() ,求△
,求△![]() 的面积;
的面积;
(3)证明:△![]() 为直角三角形.
为直角三角形.
参考答案
1、 填空题
1. 2 2. ![]() 3. 6 4.
3. 6 4. ![]()
5. 2 6. ![]() 7.
7. ![]() 8.
8. ![]() ,
,![]()
9. ![]() 10. 1 11.
10. 1 11. ![]() 12. 1
12. 1
2、 选择题
13. C 14. B 15. B 16. B
3、 解答卷
17.(1)![]() ;(2)
;(2)![]() .
.
18.(1)![]() ;(2)
;(2)![]() .
.
19.(1)![]() ;(2)
;(2)![]() .
.
20.(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() 或
或![]() ;
;
(3)![]() 或
或![]() .
.
21.(1)![]() ,轨迹是以
,轨迹是以![]() 、
、![]() 为焦点的椭圆;(2)
为焦点的椭圆;(2)![]() ;(3)证明略.
;(3)证明略.







